¶ Vérification topologique et prétraitement avant simulation
Il peut arriver qu'en cours de construction d'un modèle, on veuille déconnecter une partie du réseau (soit en ne le rattachant pas au reste du modèle, soit en l'isolant par canalisations fermées, vannes fermées ou stabilisateur de pression aval avec pression de consigne nulle).
Ces portions de modèles, si elles n'ont pas de référence piézométrique, déstabilisent et ralentissent les calculs, voire les faussent.
¶ Vérification topologique des parties de réseau : couche “sans piezo”
Express'eau effectue une vérification topologique des données du réseau :
- Recherche des parties du réseau non rattachées au reste du réseau et sans référence piézométrique.
- Recherche des parties du réseau isolées (canalisations fermées, vannes fermées ou stabilisateur de pression aval avec pression de consigne nulle) du reste du réseau et sans référence piézométrique.
Ces parties du réseau sont signalées au modélisateur dans la couche “sans piezo”.
¶ Prétraitement avant simulation
Les parties du réseau présentes dans la couche “sans piezo” ne sont pas envoyées au moteur de calcul. Cela inclut les canalisations fermées, vannes fermées ou stabilisateur de pression aval qui sont responsables de la déconnexion d'une partie du réseau.
Attention : si des éléments responsables de la déconnexion d'une partie du réseau sont cités par le fichier de régulation (par exemple pour les ouvrir), il y aura un message d'erreur du moteur qui ne connaitra pas ces éléments. Il est donc primordial de les paramétrer comme “ouverts” dans la base pour conserver la partie du réseau dans la simulation et actionner les éléments en question.
¶ Principe de la méthode de résolution
¶ Discrétisation des équations
¶ Sur les liaisons
Chaque liaison est régie par deux équations :
- L’équation de continuité : F1 (Q, Z) = 0.
- L’équation de quantité de mouvement : F2 (Q, Z) = 0.
(Q, Z) sont les variables inconnues de la liaison en un point courant de la liaison.
Chacune de ces équations est discrétisée suivant le schéma implicite de Preismann :
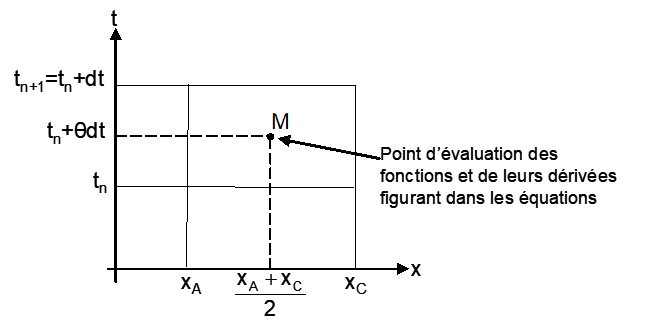
Où :
- A est le point amont et C le point aval de l’élément hydraulique discrétisé.
- θ est compris entre 0,5 et 1
L’algorithme de discrétisation est le suivant :
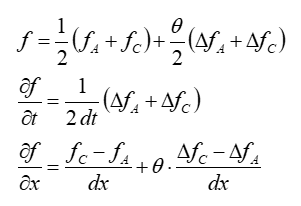
Avec :
- fA est la fonction évaluée au point A à un instant donné.
- fC est la fonction évaluée au point C à un instant donné.
- ΔfA = fA(t+dt) - fA(t)
- ΔfC = fC(t+dt) - fC(t)
Après discrétisation du système d’équations entre les points extrémités amont A et aval C de la liaison, on obtient un système linéarisé d’ordre 1 sous la forme matricielle suivante pour chaque liaison :
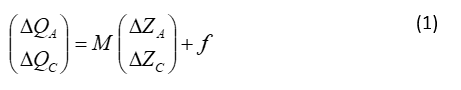
Où :
- les coefficients de la matrice M et du vecteur f sont calculés au temps t et :

- QA(t) est le débit entrant dans la liaison au point A (idem pour le point C),
- ZA(t) est la cote piézométrique au point A (idem pour le point C),
- dt est le pas de temps.
¶ Sur les singularités
Chaque singularité est quant à elle discrétisée sous la forme :
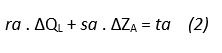
où les coefficients ra, sa et ta sont évalués au temps t.
¶ Assemblage des équations discrétisées
Les variables de débit sont éliminées en écrivant que la somme algébrique des débits aboutissant à un nœud donné est nulle. On obtient ainsi un système matriciel global de la forme :
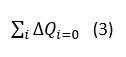
Où Qi désigne un débit sortant (compté positivement) ou rentrant (compté négativement) d’une liaison connectée au nœud.
La substitution des équations (1) des liaisons dans les équations (2) fournit le système matriciel global suivant :
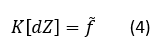
où :
- K est une matrice carrée de rang N, N étant le nombre total de nœuds du modèle,
- f est un vecteur force de dimension N,
- dZ est la variation de cote piézométrique à chaque noeud entre deux pas de temps.
Le système matriciel (3) est résolu à l’aide du solveur « Pardiso » réputé pour sa précision et sa très grande rapidité.
La connaissance du vecteur [dZ] permet de calculer les nouvelles cotes (Z) à chaque nœud au temps tn+1, puis les débits (Qa, Qc) à l’extrémité de chaque liaison à l’aide des équations (1) et (2).
Avec cette méthode l'équation de continuité aux nœuds est rigoureusement satisfaite à chaque itération.
¶ Adaptation de la méthode à chaque mode de calcul
¶ Pour le calcul en régime établi
La méthode de discrétisation décrite ci-dessus ne convient que si la distribution initiale (Qi,Zj) rentrée par l’utilisateur est proche de la solution exacte, ce qui en pratique est irréalisable puisque l’on ne connait pas la solution au démarrage des calculs. Le schéma de discrétisation de Preisman est dans ce cas remplacé par un schéma beaucoup plus robuste inspiré de la méthode de la sécante et qui converge vers le schéma de discrétisation de Preisman quand la solution calculée devient proche de la solution vraie.
La solution est obtenue par itération successives, chaque itération correspondant à un pas de temps fictif. Le nombre d’itérations requises pour approcher la solution en cote avec une tolérance de 1 cm sur les écarts entre deux itérations, est de l’ordre de 5 pour les réseaux de quelques centaines de nœuds et 10 pour les réseaux de plusieurs milliers de nœuds : la convergence est donc très rapide.
¶ Pour le calcul en régime transitoire graduellement varié
Le schéma de discrétisation de Preisman est appliqué entre deux pas de tems successifs, sauf lorsque les écarts en cotes sont trop importants. Dans ce cas le schéma de résolution devient itératif jusqu’à obtention de la convergence pour le pas de temps en cours. La gestion de la méthode est automatique dans le programme.
A noter que le mode 1 est précédé au premier pas de temps d’un calcul itératif d’équilibrage en mode 0, de façon à démarrer le calcul transitoire avec des conditions initiales équilibrées.
Si l’option de calcul de qualité est affichée le pas de discrétisation spatiale est ramené en interne à 20m (comme dans le mode 2 ci-après), de façon à limiter les effets de dispersion numérique du front de concentration.
¶ Pour le calcul en régime transitoire rapidement varié
Deux différences importantes avec le mode ci-dessus :
- Le pas de discrétisation le long d’un tronçon de canalisation est limité à 20 m ; autrement dit le programme ajoute automatiquement des nœuds de calculs intermédiaires pour reproduire correctement la propagation des ondes de pression,
- Le programme détecte les modifications rapides de position d’organe. A chaque nouvelle détection il applique localement les équations des « caractéristiques » autour de l’organe et modifie la solution du pas de temps précédent en tenant compte des discontinuités générées par la manœuvre subite. La discontinuité est propagée ensuite à l’aide du schéma de discrétisation de Preisman.
Supposons pour illustrer la méthode le cas d’une fermeture rapide de vanne en travers d’une canalisation :
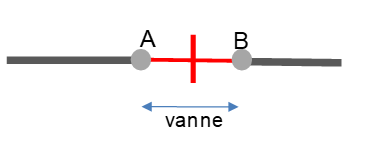
Les valeurs (QA, ZA, QB, ZB) sont modifiées par résolution du système local d’équations suivant :

C0 est la vitesse de propagation de l’onde de pression et U la vitesse d’écoulement dans chaque conduite de part et d’autre de la vanne.
La fonction d’orifice f est exprimée avec la nouvelle section d’ouverture. La résolution locale de ce système a pour conséquence de générer un saut de pression (ZA’-ZA) et (ZB’-ZB) au point A et au point B respectivement, ce saut étant propagé aux pas de temps suivants par l’algorithme général de résolution implicite.
¶ Gestion des discontinuité
Les coups de bélier (ou discontinuités de pression) sont générés par des manœuvres brusques d’organes ou par des changements d’états brutaux de fonctionnement. Le tableau ci-dessous récapitule les organes susceptibles de générer des coups de bélier et le mécanisme de génération associé.
| Désignation | Organe | Mode de génération du coup de bélier |
| POMP | POMP | Rupture brutale d’alimentation électrique |
| CLPT | Clapet | Fermeture brutale du clapet |
| VANNE | Vanne plate | Fermeture brutale de la vanne |
| REGQ | Vanne de régulation de débit | Fermeture brutale de la vanne |
| REDP | Vanne de régulation de pression | Fermeture brutale de la vanne |
| Q0 | Prélèvement/injection de débit | Variation brutale du débit |
| BALL | Ballon anti-bélier | Fin de vidange du ballon |
| VNTS | ventouse | Fin d’évacuation de la poche d’air admise dans le réseau |
Le mécanisme générateur du coup de bélier dépend du type d’organe :
¶ Les vannes, les régulateurs
Pour les vannes l’utilisateur doit fournir une courbe temporelle de décroissance du taux d’ouverture de la vanne. La courbe de décroissance a l’allure suivante :
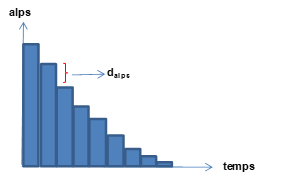
La courbe de décroissance est discrétisée en forme en marches d’escalier, faisant apparaitre une série de sauts élémentaires. Le programme applique l’algorithme du paragraphe précédent à l’instant où le saut se produit, ce qui génère une petite discontinuité de pression à chaque borne de la vanne. Une nouvelle discontinuité de pression est générée à chaque nouvel instant où un saut de section d’ouverture est rencontré sur la courbe, l’accumulation de ces sauts est susceptible d’engendrer ou non un coup de bélier détectable selon les temps relatifs de fermeture de la vanne et de propagation des ondes dans le réseau.
¶ Les clapets
Deux options sont disponibles : dans une option le programme détecte lui-même l’instant où la direction de l’écoulement s’inverse et applique alors la courbe de fermeture rentrée par l’utilisateur ; cette fonction est définie par l’utilisateur en fonction des caractéristiques mécaniques du clapet et des conditions hydrauliques ambiantes.
Dans l’autre option l’utilisateur définit lui-même l’instant de démarrage de la fermeture s’inverse et applique alors une courbe de fermeture.
En pratique la première option est généralement appliquée.
A noter que si un objet Clapet est défini en aval d’une pompe il faut s’assurer que l’option « clapet » est désactivée dans l’élément Pompe.
¶ Les pompes
Deux options sont disponibles :
- dans une option l’utilisateur rentre uniquement l’instant de la disjonction électrique. Le programme applique alors la courbe de décroissance de la vitesse de rotation de la pompe définie dans son paramétrage (voir ici).
- Dans l’autre option l’utilisateur définit lui-même la courbe temporelle de décroissance de la vitesse de rotation après disjonction.
¶ Les débits injectés
L’utilisateur définit une courbe temporelle de décroissance du débit initialement injecté. Chaque saut élémentaire de débit provoque une discontinuité de pression ; on est ainsi ramené aux 2 cas ci-dessus.
¶
¶ Fin de vidange d’un ballon anti bélier, fermeture brutale d’un clapet anti retour
Dans ce cas la discontinuité de fonctionnement n’est pas générée par une courbe prédéfinie mais elle est détectée par le programme à l’instant où un ballon en phase de vidange se vide totalement : le débit de vidange QL juste avant la mise à sec du ballon devient brusquement nul, ce qui génère le coup de bélier. La détection et la gestion de cet événement possible au cours du calcul est totalement prise en charge par le programme. En pratique on dimensionne le volume du ballon pour éviter de provoquer ce type de phénomène qui peut être très destructeur.
L’instant de la fermeture totale d’un clapet anti retour génère également une surpression brutale, communément appelée « coup du clapet ». Cette surpression est conditionnée par l’allure de la courbe de fermeture définie par l’utilisateur. Dans le cas d’une fermeture très rapide dès la détection d’une inversion d’écoulement aucune surpression n’est générée.
¶ Fin d’évacuation de la poche d’air par une ventouse
Le mécanisme de génération du coup de bélier est analogue à celui du ballon : l’onde de pression provoque l’expulsion de la poche d’air créée par le passage antérieur d’une onde de dépression. Cette expulsion est vue par le réseau comme un soutirage d’eau avec un débit équivalent QL. Au moment où la poche d’air se vide totalement le débit QL devient brusquement nul, ce qui génère un coup de bélier. Afin de minimiser ce phénomène également gênant, on sélectionne généralement une ventouse avec un diamètre d’orifice adapté par rapport au diamètre de la canalisation. Ce point est précisé ici.